Utiliser une sonde pour calibrer ses écrans

2. Représentation des couleurs

Avec l´utilisation des ordinateurs, nous avons l´habitude de décomposer les couleurs en composantes rouges, vertes et bleus. En pratique, c´est un peu plus compliqué, puisque les couleurs sont en fait perçues par notre oeil comme un mélange de différentes contributions à différentes longueurs d´onde λ dans le domaine 380-780 nm. Afin de mieux comprendre ce qu´il se passe quand on calibre un écran, il est donc important de savoir comment on représente les couleurs, et pourquoi seules certaines couleurs sont accessibles quand notre oeil pourrait en détecter davantage. De même, certains termes techniques (température, Gamut) nécessitent quelques explications pour bien comprendre comment étalonner.
Pour faire simple, une couleur sera systématiquement représentée par un triplet (R,V,B), (X,Y,Z), (L,a,b), (u, v, Y), (x,y,Y), ... en fonction de la façon dont on va les représenter. Le triplet (X,Y,Z) joue un rôle plus particulier puisqu´il sert de référence pour construire tous les autres triplets.

Pour chacun des systèmes de coordonnées, un Gamut désigne le volume des couleurs que l´on peut produire.

Calcul des couleurs : observateur standard et tristimuli (X,Y,Z)

L´oeil humain est en fait constitué de différents capteurs, plus ou moins sensibles à certaines longueurs d´ondes (cônes, bâtonnets). Bien que chaque oeil soit finalement unique, différents observateurs standards on été définis par moyennage statistique sous différentes conditions expérimentales. Evidemment, ont été exclus toutes personnes atteintes de daltonisme. Ces étalons ont été exposés sous conditions contrôlées (angle d´incidence, puissance lumineuse etc.) à des signaux lumineux de différentes longueurs d´ondes, permettant ainsi de construire trois courbes spectrales appelées Color Matching Functions qui sont très étroitement liées aux gammes de détection des différents capteurs de l´oeil humain. Ces trois fonctions, x(λ), y(λ), z(λ) ont été construites et définies à différentes reprises et un consortium (CIE) a cherché à définir différentes normes :

• en 1931 pour l´observateur exposée à de la lumière avec au plus 2 degrés d´incidence, puis rafraichies en 1951 et 1978 : c´est ce qu´on appelle l´observateur standard CIE-1931 2-degrés.
• en 1964 pour l´observateur exposée à de la lumière avec au plus 10 degrés d´incidence : c´est ce qu´on appelle l´observateur standard CIE-1964 10-degrés.

De ces deux "observateurs", le premier est celui qui est le plus utilisé. Ceci étant, les Color Matching Functions qui en découlent sont très proches. Celles pour l´observateur CIE-1931 2-degrés sont données dans la figure ci-dessous.

Fig.1 - Color Matching Functions pour l´observateur standard CIE-1931 2-degrés

Ces fonctions constituent la brique angulaire indispensable pour calculer une couleur et sont étroitement liées à la perception des couleurs primaires rouges, vertes et bleues, notamment y pour le vert. En effet, si on considère une source lumineuse S(λ) qui est réfléchie sur une surface avec un coefficient de réflexion R(λ), on peut alors calculer un premier triplet (X,Y,Z) pour représenter les couleurs :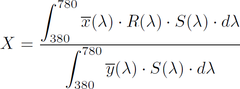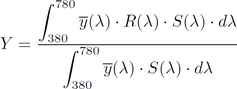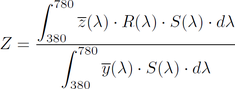

Pour l´oeil humain, la luminosité est confondue avec la détection de la couleur verte : pour cette raison, c´est la quantité Y qui la représente. Celle-ci varie nécessairement entre 0 et 1 puisqu´un coefficient de réflexion R est forcément compris sur ce même intervalle. Les quantités X et Z sont elles aussi majorées par des constantes qui dépendent du spectre de la source S considérée.

On pourra noter que le calcul d´une couleur dépend donc :

• de l´observateur standard utilisé : c´est un des paramètres avancés à considérer lorsqu´on étalonne (DisplayCal permet d´en sélectionner 8 différents au besoin)
• du spectre de référence utilisé pour S(λ) : ce second paramètre est particulièrement important est dépend de ce qu´on appelle la température (expliquée plus loin)

Représenter (X,Y,Z) n´étant pas chose aisée car il s´agit d´un volume borné, dont les bornes dépendent du spectre S pour les composantes X et Z. Différentes stratégies de conversion ont donc été mises en place pour faciliter la représentation des couleurs. Pour que les explications restent accessibles, on se restreindra à la conversion vers l´espace CIE 1931 (x,y,Y).

Diagramme CIE 1931 xyY

C´est un des tous premiers diagrammes construits pour faciliter la représentation des couleurs. La luminosité étant contenue dans Y, la première piste a dont été de représenter "simplement" la chromaticité d´une couleur : en gros, les nuances de couleurs, indépendamment du fait qu´elles soient lumineuses ou sombres (puisque c´est Y qui contient cette information). Il a donc fallut opérer un changement de coordonnées, ce qui permet d´introduire x et y (à ne pas confondre avec les Color Matching Functions) calculés comme suit :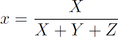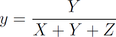

Par définition, x et y évoluent dans un espace borné entre 0 et 1. Les couleurs pures (constituées d´une seule longueur d´onde) balaient alors une courbe en forme de "langue de chat" qui part du point λ=380 nm en bas à gauche, à λ=780 nm plus à droite (fig. 2).

Fig.2 - plan chromatique (x,y) du Gamut CIE 1931

On peut noter que la graduation tous les Δλ=10 nm n´est pas représentée par la même distance sur courbe des couleurs pures : les zones vertes sont dilatées, tandis que les début et fin de courbes sont relativement "tassés" avec des graduations bien plus proches. C´est une forte limitation de cet espace de couleurs : il n´est pas normé. On ne peut donc pas y calculer la distance entre deux couleurs : ce n´est donc pas dans l´espace (x,y,Y) qu´on calcule les quantités ΔE.

Le convexe délimité par les couleurs pures représente l´ensemble des couleurs perceptibles. En effet, si on considère plusieurs raies, la couleur obtenue sera un "mélange" des couleurs pures pondérées par leurs intensités respectives. Ainsi, le mélange de deux raies de réflection à 500 et 620 nm donne une couleur quelque part sur le segment délimité aux extrémités par les couleurs pures à 500 et 620 nm respectivement. On peut généraliser à plusieurs raies, et donc un spectre réfléchi R(λ). Le segment entre les points de longueurs d´onde 380 et 780 nm définit ce qu´on appelle la purple line ou Ligne du violet puisqu´il s´agit du mélange du rouge et du bleu.

Point blanc, température et illuminant

Par définition, une surface sera blanche si R(λ)=1 sur l´ensemble du spectre dans les différentes formules permettant de calculer (X,Y,Z) et par conséquent (x,y,Y). Comme indiqué plus haut, le calcul d´une couleur dépend de la source S considérée : c´est aussi le cas pour le blanc. Il a donc fallu considérer un spectre de référence : en dehors des éclairages artificiels, c´est donc le soleil qui est le plus souvent notre référence. Malheureusement, ce spectre est partiellement absorbé par l´atmosphère terrestre : lorsqu´il éclaire différent objets, son contenu spectral n´est donc pas toujours le même et dépend :

• la latitude et l´heure de la prise de vue, qui impactent directement l´épaisseur d´atmosphère que traversent les rayons solaires.
• la qualité de l´atmosphère elle-même, et donc des conditions météorologiques (et désormais aussi de la pollution).

La distance terre-soleil n´a pas d´impact sur les couleurs, puisque l´ensemble du spectre de la source S est pondéré par un même facteur : au premier ordre, une loi quadratique avec la distance terre-soleil.

Une autre solution consiste à utiliser des sources de lumières standardes pour obtenir une température de couleur corrélée (TCC). En principe, si on chauffe un filament à une certaine température (par exemple, un fil de tungstène qu´on place dans le vide, dont on connait le diamètre et qu´on expose à un courant donné... soit une ampoule !), sa surface émet de la lumière selon un spectre qu´on peut assimiler à celle émise par un corps noir. Ce dernier s´exprime de la forme suivante :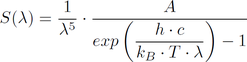

où A est une constante. C´est la loi de Planck, illustrée en figure 3 pour différentes températures T, dont celle à la surface de la terre (300 K) et à la surface du soleil (5777 K).

Fig.3 - Rayonnement d´un corps noir à différentes températures

Plus la température sera élevée en Kelvin, et plus la quantité de bleu par rapport au rouge va augmenter dans la source de référence S(λ). Ainsi, une même surface blanche éclairée par une lampe à haute température T pourra apparaitre bleutée, tandis qu´elle apparaitre plus rougeâtre avec une source de plus basse température. Contre intuitivement, on parle d´éclairage plus froid quand il est bleuté, alors qu´en fait la source d´éclairage est en faite... plus chaude ! De même, on peut calculer les coordonnées (x,y) d´une surface blanche (R(λ)=1) pour différentes températures d´éclairage T : c´est la courbe graduée en Kelvin placée dans la figure. 2, qu´on appelle lieux planckiens. On retrouve ainsi que les fortes températures (T=+∞) sont en faite bleutées, lorsque la température diminue, on rejoint lentement le point rouge en λ=780 nm. En photographie, ajuster la balance des blancs, c´est donc trouver le corps noir qui se comporte au plus près de la source de lumiére qui éclairait la scène. L´éclairage utilisé n´étant pas forcément sur la courbe des lieux planckiens, la plupart des logiciels disposent d´un ajustement de teinte en plus de la température.

Plusieurs illuminants ont été utilisés pour définir les couleurs (il en existe d´autres, comme A, B, C, F1.. F12, en fonction des applications utilisées):

• D50 : pour un corps noir à 5003K et se rapproche du comportement du soleil sur terre en lever et coucher de soleil
• D55 : pour un corps noir à 5503K et se rapproche du comportement du soleil sur terre en milieu de matinée ou après midi
• D65 : pour un corps noir à 6504K et se rapproche du comportement du soleil sur terre au zénith

On pourra noter que les températures ci-dessus ont évoluée : initialement, il s´agissait de 5000, 5500 et 6500K respectivement mais la re-définition de la constante de Planck en 1968 a légèrement impacté les températures considérées.

Triangle sRGB et autres espaces (R,G,B)

Pour nos écrans d´ordinateur et définir les espaces de couleur, c´est le point D65 qui a été considéré comme référence. Comme expliqué dans la première partie, le rétro-éclairage n´est pas constitué de trois sources monochromatiques pour le rouge, le vert et le bleu, ce qui en réduit la saturation. Il a donc été historiquement décidé que les écrans (tubes cathodiques) travailleraient avec les moyens du moment à des couleurs moins saturées. Ainsi, les points suivants ont été considérés :

	x	y	λ	Code sRGB
Blanc (D65)	0.3127	0.3290	-	(255,255,255)
Rouge (R)	0.6400	0.3300	612 nm	(255,0,0)
Vert (V)	0.3000	0.6000	547 nm	(0,255,0)
Bleu (B)	0.1500	0.0600	464 nm	(0,0,255)

... et on constate bien que la demi droite passant par D65 et le point V intersecte bien les couleurs pures à la longueur d´onde λ de 547 nm. Le vert utilisé sur nos écrans est donc moins saturé que le vert parfait de 547 nm. Par combinaison linéaire, seules les couleurs à l´intérieurs du triangle RGB peuvent être affichées, c´est l´espace de couleur sRGB de nos écrans, qui est aussi commun à nos appareils photo et caméras lorsqu´ils sont réglés pour l´utiliser.

Pour étendre davantage le nombre de couleurs affichables, certaines appareils utilisent d´autres définitions des points (R,V,B). Par exemple, pour le format adobeRVB (aRVB), le point vert est davantage saturé (fig. 4). Cependant, ces espaces particuliers ne sont pas nativement exploités par nos ordinateurs : pour profiter pleinement des 255 nuances par canal, il est préférable de travailler sur le plus petit espace commun à tous les appareils qu´on utilise, ce qui sera sRGB le plus souvent.

Fig.4 - Comparaison des espaces chromatiques entre sRGB et aRGB

On pourra noter que l´espace sRGB intersecte les lieux planckiens vers 2000K : c´est pour cette raison que la plupart des logiciels de traitement d´image ne permettent pas d´utiliser une température plus basse lorsqu´on corrige la balance des blancs : aller au delà n´aurait en fait aucun sens si on affiche sur un moniteur.

NB :

Si on configure son appareil photo pour travailler en adobe RGB, et qu´on affiche les couleurs sur un écran réglé en sRGB (espace par défaut des écrans), soit on n´utilise qu´une partie des 255 valeurs du canal vert (on perd en dégradé), soit on recale le vert de l´aRGB sur celui de sRGB (on conserve les dégradés, mais on perd en saturation dans les verts : la compenser revient au cas précédent). Les deux comportements peuvent arriver en fonction des logiciels utilisés et de la gestion des profils de couleur. Dans le cas des fichiers RAW avec 12-14 bits par canal, le problème est similaire mais le nombre plus important de nuances permet de compenser ce problème. Mais dans tous les cas, on perdre de l´information à un moment.

Autres espaces de couleur

Comme indiqué plus haut, l´espace (x,y,Y) n´est pas normé : on ne peut donc pas calculer une distance dans cette espace là, bien qu´il soit très pratique pour représenter les couleurs, puisque les couleurs pures se trouvent toutes dans un même plan. L´espace CIE 1931 xyY est aussi un espace absolu : la position d´une couleur ne dépend pas d´un point de référence (comme D65). L´un des principaux espaces utilisée est CIE L^*a^*b^* 1976 (où L est la clarté, information proche de la luminosité), qui est à la fois normé (on peut calculer un volume, ou une distance ΔE), et relatif (d´où les étoiles dans le nom des composantes) par rapport à l´illuminant D65. Travailler avec un autre illuminant que D65 est donc une mauvaise idée dans ce cas. Les frontières du domaine sRGB correspondent alors au volume de la fig. 5.

Fig.5 - Représentation de l´espace sRGB en coordonnées CIE L^*a^*b^* 1976

Au sens de la norme L^*a^*b^*, la distance entre deux couleurs est donc ΔE₇₆=[(ΔL^*)²+(Δa^*)²+(Δb^*)²]^1/2. Cette norme n´étant pas parfaite, d´autres définitions ont vue le jour en pondérant les trois composantes et en les écrivant en coordonnées cylindriques (espace CIE L^*C^*h^* 1976, où L est la même clarté que pour CIE L^*a^*b^* 1976) et non pas cartésiennes.

Principaux réglages pour calibrer et étalonner ses écrans

Suite aux explications, il découle que les principaux éléments à régler sont les suivants :

• La température du point blanc : 6500 K. Comme D65 est utilisé comme référence dans les normes servant à calculer les erreurs, et que c´est aussi le point de référence de l´espace sRGB, il est très fortement conseillé de ne pas changer cette valeur.
• Gamma : 2.2. Ce paramètre n´a pas été détaillé. Il s´agit d´une constante qui permet de corriger le comportement de notre oeil qui se comporte plutôt comme un détecteur logarithmique.
• La luminosité du point blanc : 120 Cd.cm^-2 est la valeur généralement admise. On pourra l´ajuster en fonction de la luminosité de la pièce où l´on se trouve.
• Le type de rétro-éclairage utilisé : on pourra utiliser l´excellent site Display Specification pour l´identifier.

Le calibrage consiste donc à afficher un carré blanc (255,255,255) sur son écran et en mesurer la température. L´ajustement des gains et de la luminosité de l´écran sert à faire en sorte à qu´elle coïncide avec 6500 K (D65) au niveau de luminosité souhaité.